新年伊始,很荣幸笔者的专栏在慕课专栏板块上线了,欢迎大家订阅!为了能够提供给大家更轻松的学习过程,笔者在专栏内容之外会陆续推出一些手记来辅助同学们学习本专栏内容,因此同学们无需担心专栏内容在学习上的困难,更多的是明确自己学习的目的即可。当然笔者也欢迎同学们踊跃留言,说出自己想扩展的知识点,笔者会根据同学们的意愿选择性的推出一些内容。
在第一篇中笔者结合一个简单的市场模型介绍了为什么在没有概率优势的前提下参与交易会亏钱,其实股票交易和玩一个游戏、做一个项目理念是相通的,需要章法、需要制定策略,否则就和抛硬币赌博一样一样的,用量化交易可以帮助我们管理好概率,更理性的去下单。
在第二篇中笔者在专栏《股票交易策略开发:走势线性回归选股策略》小节的基础上对线性回归方法的策略应用做进一步的扩展介绍。由于线性回归作用于股票收盘价的整个周期,前后两段完全相反的周期会彼此作用,最终影响拟合的角度值,于是笔者设定窗口期用移动窗口的方式拟合股价的走势,寻找角度曲线的拐点以预示新一轮的反转走势,给大家提供一个衍生的策略思路。
在第三篇中笔者在专栏
《股票交易数据可视化:买卖区间下策略收益绘制》的基础上对策略的最大回撤指标做一定的扩展介绍。投资是有风险的,那么如何去衡量这个风险呢?最大回撤率就是一种直观的将风险切实量化的指标,它描述了买入股票后,在策略出现最糟糕的情况下会损失多少钱,这也直接关系到了风险策略中止损因子的设定。————————————————————————————————————————本次场外篇笔者在专栏《19、股票交易策略开发:趋势突破择时策略》的基础上对寻找最优化策略参数的方法做一些扩展介绍。在开发交易策略的过程中常常会涉及到选择哪个参数的问题,比如均线指标有M20、M30……经过N日平滑形成,在围绕均线展开的趋势型策略中不同的均线最终所产生的回测效果也是不一样的。在单均线突破的交易策略介绍中,笔者分别用指示短线操作的M20和指示中长线操作的M60两种移动平均线作为策略参数进行回测,最终从收益曲线上可以看出应用M60作为策略参数效果更好,不仅交易次数明显减少,亏损也大幅度减少。但是M60真的是最优化参数了吗?好像也不见得,那么让我们在之上一步一步地开始寻找最优化参数之旅吧!!
对于寻找最优化参数的方法可以选择枚举法或者蒙特卡洛法。枚举法也称为列举法、穷举法,它的基本思想顾名思义就是逐一列举所有可能的情况,并且一个不漏地进行检验,从中找出符合最佳要求的答案。虽然枚举法得到的结果肯定是正确的,但是为了换取答案的全面性却牺牲了很多无用的时间,只能适用于解决效率要求不高,样本规模小的问题。蒙特卡洛这类方法的特点是在随机采样上计算得到近似结果,随着采样的增多,得到的结果是正确结果的概率逐渐加大,但在遍历全部样本之前,无法知道目前得到的结果是不是真正的结果。蒙特卡洛法不同于枚举法的应用,它为了提高搜索的效率却牺牲了答案的全面性,因此它得到的结果并不一定是最优的,但是在大规模样品的场合下可以更快地找到近似最优结果。此处我们仅仅需要寻找出在M20至M60之间的最优均线参数,因此枚举法更合适。
我们只需对单均线突破策略的回测代码class QuantAverBreak进行改造,将移动平均线窗口值开放为变量传入run_factor_plot()方法中,另外去除绘图相关的plt代码,增加返回最终收益值代码。
class QuantAverBreak: def __init__(self): # 仅体现更改代码 def run_factor_plot(self, stock_df, N): stock_df['Ma_n'] = stock_df.Close.rolling(window=N).mean() # 增加移动平均线 list_diff = np.sign(stock_df.Close - stock_df.Ma_n) return stock_df['profit'][-1]
接下来我们遍历参数20至60,将参数作为移动平均线的窗口值传入策略中,最终返回回测后的资金收益结果,我们以图表的方式对比选择出资金收益最高的参数作为最优化的参数。
例程代码如下所示:plt.figure(figsize=(25, 12), dpi=80, facecolor="white")ma_list = []profit_list = []for ma in range(20, 60): examp_trade = QuantAverBreak() ma_list.append(ma) profit_list.append(examp_trade.run_factor_plot(stock, ma))profit_max=max(profit_list)print(profit_list.index(max(profit_list)))ma_max=ma_list[profit_list.index(max(profit_list))]plt.bar(ma_list, profit_list)plt.annotate('最优参数ma='+str(ma_max)+'\n profit='+str(profit_max),\ xy=(ma_max,profit_max),xytext=(ma_max-10, profit_max-10),arrowprops=dict(facecolor='yellow',shrink=0.1),\ horizontalalignment='left',verticalalignment='top',fontsize=20)# 设置刻度字体大小plt.xticks(fontsize=20)plt.yticks(fontsize=20)# 设置坐标标签字体大小plt.xlabel('均线参数',fontsize=20)plt.ylabel('资金收益',fontsize=20)# 设置坐标轴的取值范围plt.xlim(min(ma_list)-1, max(ma_list)+1)plt.ylim(min(profit_list)*0.99, max(profit_list)*1.01)# 设置x坐标轴刻度plt.xticks(np.arange(min(ma_list), max(ma_list)+1, 1))# 设置图例字体大小plt.legend(['profit_list'], loc='best', fontsize=20)plt.title("均线最优参数",fontsize=50)plt.show() 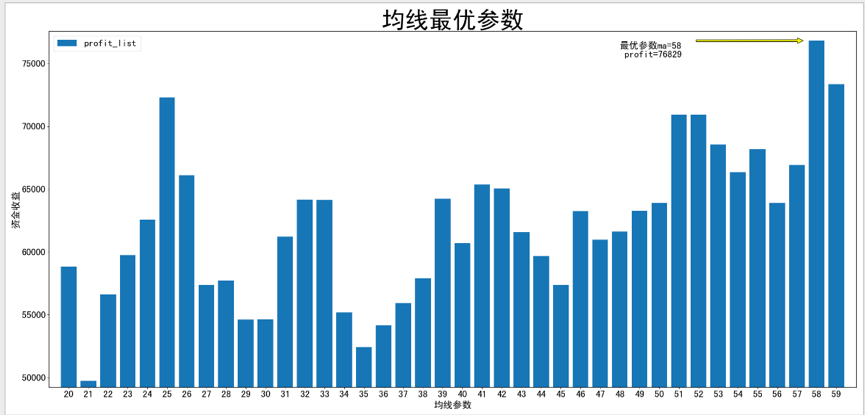
从结果中我们看到资金收益最高时为76829元,所对应的移动平均线的最优参数是58日,但是我们模拟的初始资金可是10万元啊,这么看应用了策略和优选参数后最终的资金仍然是亏损的,这如何解释呢?关于这点笔者毫不避讳展示回测的真实结果,目的就是拒绝过度拟合以给大家一个量化交易可以无所不能的错觉。其实,回测的本质作用就是反映策略和参数在过去某段时间的市场中是盈利还是亏损的,以评价策略和参数的好坏,很明显17年至今A股市场一直处于下跌的态势,或许我们不采用量化策略会亏损的更多。话说回来我们也是有更多的选择,可以选择不交易,也可以选择更好的股票和更好的策略进行交易!